Complex Algebra

Suppose the analysis of an electical circuit in steady sinusoidal AC (for example), requires that we perform a variety of complex algebra manipulations. Such as:

Checklist:

• is your calculator on?
• are you on the HOME screen?
• is the cursor on the Entry Line?
• is the Entry Line empty?
• are you in Angle: RADIAN mode?
• are you in Complex Format: RECTANGULAR mode

Sometimes it is easy to represent a complex number in a rectangular format. That is, in a a+bi form. On other occasions, it is more natural to write complex numbers in the polar form of r<ø, and in the rest -- the mixed version of r exp(ø).

Any of the three forms can be used together with the other forms. But you must pay attention to the next important points:

• You must use paranthesis around a polar representation. i.e. always write (2<10°), and never just 2<10°.
• Beware of the illusion caused by forgetting Angle: DEGREE mode on! Check your status indicators. In DEG mode, angles are not followed by a " ° " sign, and it is very easy to mistake them for radians.
• The special symbol i is not the same as plain alpha keyboard i.
• The r exp(ø) form is both polar and rectangular since what is really written by it is both r<ø and r (cosø+isinø)

? OK... So...?

Ans Well, once you remember these simple principles, making computations with complex expressions is as easy as with "regular" real expressions! Stick around and we'll see some examples.

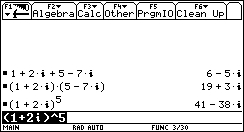
The first task requires that we add two complex expressions:

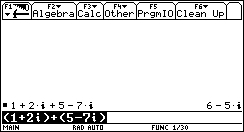
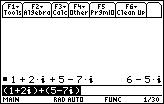
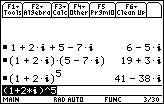
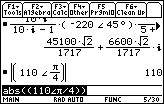
1. (1+2i) + (5-7i)

How is this accoplished on the TI-89 or TI-92(+)? Obviously the calculator must "know" how to add the real parts together and the imaginary parts together. Does it? Well, of course! To add these expressions, just type them in and press ENTER (the paranthesis are just for clarification. You don't need to add them too).

? I got something weird here...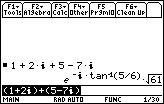
Ans Don't panic! As mentioned previously, the TI-89 or TI-92(+) has a default Complex Format specification. It's in your MODE settings dialog box. Your MODE setting for Complex Format is set to polar. That's why your calculator returned the result in polar form, and not in rectangular form. Change your MODE:Complex Format setting to rectangular:

• Press the MODE button.
• In the MODE dialog box, look at the your Complex Format setting. It's polar.
• Change the setting to rectangular.
• Now repeat the calculation. Does the result appear in the desired format now?

? Umm... I got something weird here too...

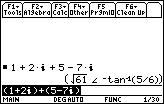
Ans No problem at all! You're in polar form, with the Angle set to degree instead of radian. Open your MODE dialog box as mentioned above, and change your Angle setting to radian, and your Complex Format setting to rectangular. Repeat the calculation. Is it in the desired format now?

Multiplication is as simple and straightforward as addition...

2. (1+2i)·(5-7i)

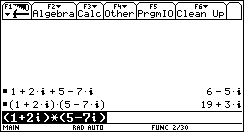
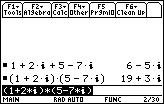
... and so is raising to a power!

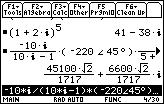
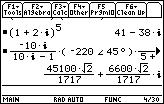
3. (1+2i)^5

1. always add paranthesis around the polar form,

2. results will be displayed in the default form, no matter is the calculation involved another form.

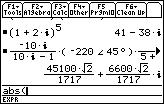
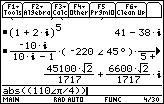
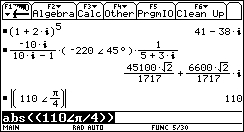
The function that calculates the absolute value of a complex/real expression is abs().

We will call the abs function with our complex expression as input, and it will return its absolute value.

1. Clear the Entry Line by pressing the CLEAR button while in the Entry Line.

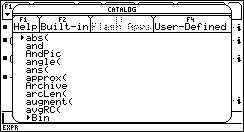
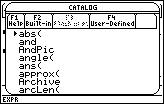
2. Open the CATALOG by pressing the CATALOG key.

3. Press the "A" key on the TI-92(+). On the TI-89: Hit the corresponding "A" key which is the "=" key (don't press or hold the alpha key!) to jump to the functions beginning with the letter "A".

? My calculator is broken! : (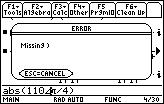

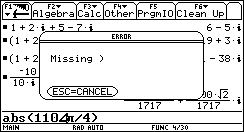
Ans No it's not. You forgot the paranthesis around the polar form!!

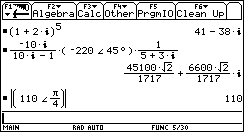
? Wait a minute! Of course the absulte value of 110<45° is 110!

Ans Oops...

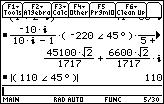
The function that calculates the angle of a complex/real expression is angle().

1. Clear the Entry Line by pressing the CLEAR key while in the Entry Line.

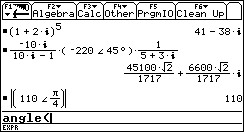
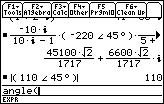
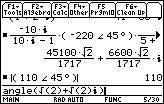
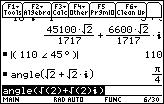
? Umm... What did I do wrong?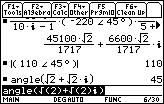

Ans Nothing. The function angle() returns angles. Therefore if you're in Angle: degree mode, you'll see 45° instead of Pi/4. Switch to Angle: radian mode and you will see the difference.