Fourier Series
The formal way of putting it: The function space can be described by
a linear combination of orthogonal functions, called a basis of that space.
When developing a function f(x) into a Taylor series, we use a base consisting
of (1, x, x^2, x^3, ..., x^n) which spans the entire function space. In
Fourier series, we simply use a different basis, a different set of orthogonal
functions to span our space. These functions are: (1, cosx, sinx, cos2x,
sin2x, ..., cosnx, sinnx).
In other words: Fourier series are a method of approximating a function, similarly
to Taylor series, but with trigonometric funcions instead of powers of x.
The Fourier series have tremendous importance in electric engineering.
In this task, we will construct a function which, under most simple conditions,
should be able to find the complete analytical expression of the Fourier series
of a function. This is a very basic progarm, intended for educational purposes
only. It will find a0, an and bn if for f(x) in the range a<x<b:
And we need to calculate:
Below: (a) for example, is a 5-element Fourier series for the function f(x)=x, while (b) is a 20-element Fourier series of f(x)=x. The peak at each end is called the Gibbs Phenomenon, and is typical of Fourier series.
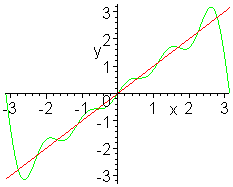 (a)
(a)
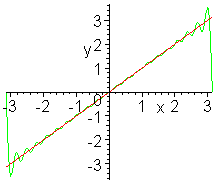 (b)
(b)
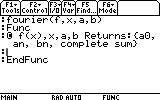
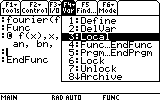
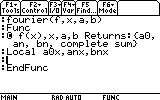
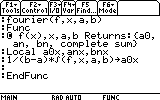
We will creat a function that recieves: f(x), x, a, b and returns: a0, an,
bn and the complete sum to the Home screen. Then we will use it to find the
Fourier series of f(x)=x, as in the examples above, and demostrate the graphical
results obtained.
Since the programming concept is faily straightfirward in this example, we
will begin writing the function immediately. In other, more complex functions,
it is recommended to make some preliminary notes of design, to better organize
the excution of the programming task.
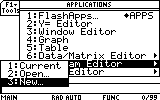
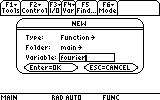
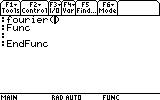
?
Oops... I forgot to make the Type a "function".
Ans
No problem, though this will be a little annoying to fix. Either quit
the editor and go back to the Home screen; there delete the function by
either typing "delvar fourier" or delete it through the Var-Link
screen; then dothe whole creation of the function again.
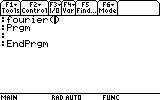
-or-
Delete the lines Prgm and EndPrgm from the editor, and choose
from the Var menu (F4) item 4:Func..EndFunc. This will define fourier
as a function, just as we want.
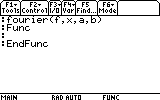
This is the program/funciton editor. Here we start by defining the function's input parameters. It will receive an expression f, which can be a function of any variable.
? How can that be? We have to know which variable because we need to put it in the integration expressions, don't we?
Ans Yes, of course we do. But here's the catch:
Suppose we let the user choose whichever variable he wants to put in f, but he must then specify that variable in the second parameter, like this: fourier(t^2, t, ..., ...). Now if we catch this second parameter in a variable, say, x, and use x throughout the function -- when the function will run it will see t everywhere instead of x, because x evaluates to t!
Back to our task, we have entered the four parameters this function receives:
? Why do you say "local" variables, and not just "variables"?
Ans
Because there're important differences between the two:
- local variables are temporary. You can
store anything into them, but they will no
longer exist when your program/function
is done.
- variables that are not local will
be actually created in the current folder, and may
by doing so delete previous
values if a variable with that name already existed, and
will remain in your current folder after
the program is done.
- local variables have to be declared
in advance using a special declaration (see
below). They also cannot be deleted., (un)archived,
or (un)locked.
- variables can be defined anytime,
deleted, (un)archived and (un)locked as the
programmer sees fit.
The last, and a very important point is that functions can use only
local variables*. This is because unlike a program, a function cannot
(among other things) write to the memory (i.e. create or modify a variable).
*Note, however, that this doesn't mean that function cannot read
from variables and use their contents. In fact, variables used for symbolic
evaluations in functions as well as in programs are required to be global.
Attempting to use a local variable for this purpose will produce an Undefined
Variable Error. (Thanks to Bhuvanesh Bhatt)
"Local" from Var menu (F4) and item 3: Local.
Now we must write down the integrals as above. This is a long but simple step. Follow the next few screenshots:
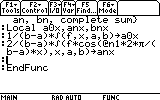
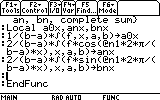
? Ok. I understand what you're doing, but what's that funny sign before "n1" there? Maybe you've got a virus on your TI??
Ans : ) No, I don't have any virus. I hope there don't exist any for these calculators yet either. That special sign is the @ sign (in case you didn't recognise it), and it is in fact an inseprarable part of the expression @n#, which has this meaning: an arbitrary integer. (Where # is 1..255) There also exists the special expression @# (where again # is 1..255), which means: any arbitrary number (integer or not). These special expressions are used by some functions on the TI89/92+. For example, the desolve function uses @# to indicate unknown constants, which are not necessarily integer. When solving trigonometric equations, the CAS usually adds @n# multiplies of Pi, to show there is an infinite number of branches belonging to the same solution. You can get the @ sign by pressing Diamond+STO on the TI89, or 2nd+R on the TI92+.
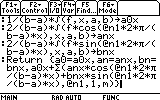
Now we write the last line, which returns the result to the Home screen.
Follow the next screenshot. The declaration
Return indicates that the following expression must be returned to
the Home screen and the function will end.
That's it! You don't need to save or anything, because everything you write
is automatically saved in the function. Press
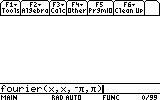
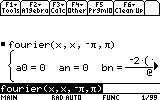
the HOME button now (Diamond+Q on the TI92+), and type the following command
on the entry line, when we would like to see the Fourier series for f(x)=x
from -Pi to Pi.
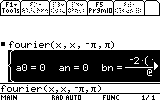
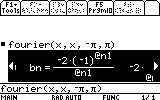
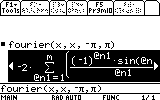
Finally, we would like to see how this approximation fits the original function.
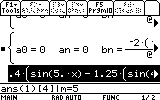
To obtain the series of f(x) up to, say, the 5th element, we simply type:
(since the resulting expressions are usually long, I recommend using Diamond+ENTER)
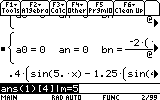
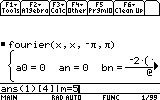
arrow key to highlight the result and Diamond+Shift on the TI89, or Diamond+C on the TI92+ to copy it. Then Press
Diamond+F1 (or Diamond+W on the TI92+) to go to the Y= Editor.
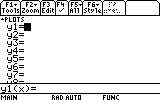
(Please clear all other functions) On y1(x) we put f(x)=x :
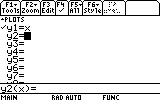
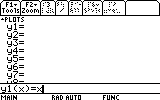
On y2(x) paste the expression (Diamond+ESC on the TI89, or Diamond+V on the TI92+):
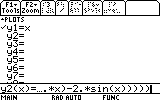
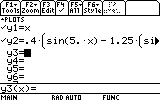
Before continuing, change the Fourier series's plotting to be with a thick line:
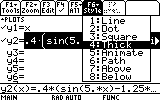
Go to the Window settings and set the following settings :
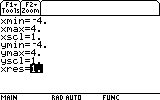
Finally, we can see the result. Go to the Graph screen now.
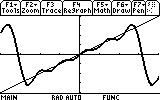
_____________________________________________________________________________________
Created by Andrew Cacovean, Nov. 17, 2001