Limits

Example No. 1: Multi-Stage Rockets

When a satelite is to be placed in orbit around the Earth, a multi-stage rocket engine is required. The reason for this is that as each stage burns out, it becomes advantageous to discard the weight of the remaining structure, thus decreasing the overall weight. When the aim is to escape Earth's gravity altogether, multi-stage design is not an option, but a necessity.

Ideally, if we could discard unnecessary weight constantly during the flight, we would have less and less mass to push away from Earth's gravity. What this means is that there would be as many stages as possible.
Theoretically, could we reach infinitely useful performance? To answer this question, let's use the limit-finding capability of the TIs to find out what happens when we design an infinite number of stages.

Our Task
Assuming identical materials used for each stage, as well as engine performance and characteristics, the expression used to tell how high the velocity the rocket will reach once all its fuel runs out is:
n is the number of stages (1, 2, 3 ... ).
r is the ratio between the entire rocket's mass and the satellite's mass, and is also a given constant (r < 1).
is a structure coefficient, given, constant and < 1.
is an equivalent velocity (which is a given constant).
when
It's hard to tell what happens to

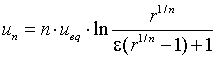
. Let's try to see what our TI thinks about it...
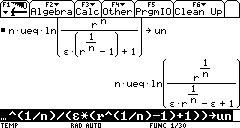
First, type in the expression and store it in a variable called un.

? Umm... Why did my TI return an unsimplified expression?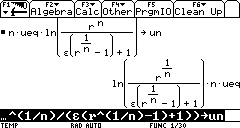

Ans Because you forgot a multiplcation sign beween the and the parenthesis in the denominator.
Don't forget that implied multiplication with the TI89 or 92+ is unnatural, because it may assume you are refering to a function call, or that your variable's name is ab while you meant a·b or even a2 when all you meant was a·2.

Now we can use the limit function to try to see what happens when

The general structure of the limit function is: limit(expr, var, point [, direction])
 expr is the expression we are working with, here the variable un. var is the variable in expr which we want to approach point. The direction will be discussed later on.

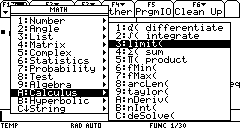
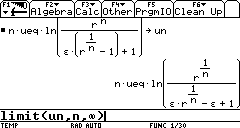
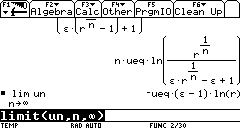
As surprising as it may seem, the result indicates that we cannot achieve an infinite velocity, even if we designed an infinite number of stages.
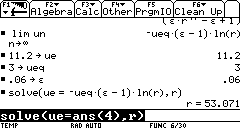
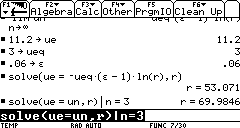
As an example, a very good ratio that we can obtain using existing technology is about 6% (this means that 6% of the entire rocket's mass is the structure). Also, for inter-planetary satellites, it is necessary to completely escape Earth's gravity field, thus un would be 11.2 km/s (36 700 ft/s). ueq, as a general rule of thumb, is around 3 km/s (9 850 ft/s). With all this information, we can deduce that at best, the ratio of rocket to satellite mass is:
This means that for every ton of satellite mass, we would require a 52 ton engine to carry it outside Earth's gravity field, 3.2 tons of which are only the structure (!). Needless to say, that in reality we never have an infinite number of stages, but only 3 (4 rarely designed). A quick calculation would reveal that for n = 3 we get:
In other words: for every ton of satellite we would need a 69 ton engine, 4.2 tons of which are only the structure!
Example No. 2: Finding One-Sided Limits

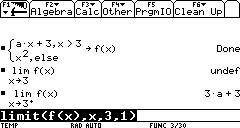
This problem is to determine whether a limit exists. The given expression:
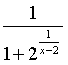
The most direct and straightforward thing to do is ask the TI to his opinion on the matter at hand:

Well, it seems our TI doesn't like it. Let's investigate this matter further. We know that a limit does not exist when the right-hand limit is not the same as the left-hand limit. Could this be what's troubling our TI?

To find a one-sided limit, we simply add a parameter to the function limit. This parameter comes last, and can be positive or negative.

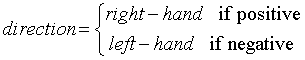
For a right-hand direction, it suffices to take 1 (in fact, any other positive number will do).
For a left-hand direction, it suffices to take -1 (in fact any other negative number will do).

First we try the right-hand limit by adding the parameter 1 to the limit function:
Next we check for the left-hand limit by changing the direction to -1:
Aha! Just as we'd suspected! The one-sided limits are not the same! Our TI was clever enough to check both directions and appropriately notify us that no limit actually exists.
Example No. 3: Finding Conditions for the Existance of A Limit for Piecewise Functions
Sometimes we may need to find the limit for a piecewise function. Cosider the following exaple: find the condition that allows for a limit of f(x) at x = 3, where f(x) is:
How do we go about solving this problem with our TI calculator? First, we must define this function.
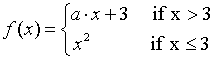
We can use the when function, to define f. The when function has the following syntax:
when(condition, true expr [, false expr [, undefined expr]])
In other words, we are declaring that when condition is true then the expression is true expr, otherwise if the condition is false then false expr. If the condition cannot be determined to be true or false, then it is undefined, in which case we instruct to use the undefined expr (this is optional, and does not have to be declared).

This is how we define our function on the TI:
Now all we need to do is see if there's a limit when x = 3, as requested:
The limit does not exist, says our TI. Let's find out in detail the reason for this. First, get the right-hand limit:
Now let's see what the left-hand limit is:
Not too surprisingly, out TI was right. Now in order for the limit to exist, we need the right-hand limit to be the same as the left hand limit. Let's solve for this equaity to get a:
And so we find out that the condition for the existance of the limit of f(x) at x = 3 is a = 2.

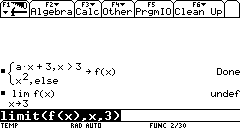
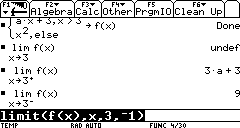
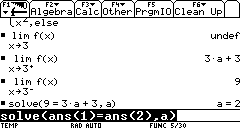
Congratulations! You have completed this task!

______________________________________________________________________________________

Created by Andrew Cacovean, March 8, 2002