Numerical Matrices
Our Task

Suppose a calculation has brought us to the following matrix:
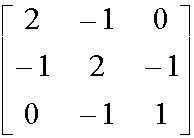
We wish to find the eigenvalues and eigenvectors of this matrix.
Step 1: Building the matrix.

Checklist:

  • is your calculator on?
  • are you on the HOME screen?
  • is the cursor on the Entry Line?
  • is the Entry Line empty?

We begin by typing in the matrix.

1. Press the APPS key.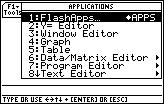

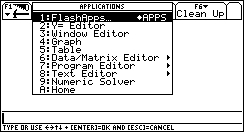
2. Scroll down to the sixth item: Data/Matrix Editor...

 

... and press ENTER.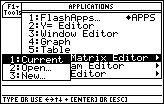

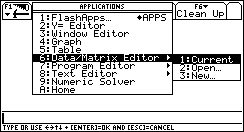
? Umm... What do I do now? Which option do I choose?

Ans You will see this sub-menu often in the APPS menu. Ask yourself these questions: I would like to work with a matrix, so...

  • Do I already have the matrix in the calc's memory? If the answer is yes, then you should choose 2: Open.
  • Is the matrix I want to work with the last matrix that was entered? If the answer is yes, then you should choose 1: Current.

Since the answer to both of these questions (in our case) is no -- this is a new matrix -- let's choose 3: New, so that we could make a new matrix.
3. In the New Data/Matrix dialog box, choose the right type of variable we wish to build: a Matrix. In the Variable text input box, type "a". Choose the correct dimensions of the matrix by entering "3" in the remaining input boxes, and finally confirm your settings. (The first ENTER will highlight the last text entered. The second ENTER will confirm the settings).
Tip: you don't really need to fill in the exact size of the matrix. You can leave it as 1x1. The size is automatically updated when you enter the numbers!

TI89 users: Wondering whether you're typing letters or numbers? Check whether the ALPHA indicator is on!

Read the manual's Chapter 2: The Keyboard.

4. Proceed by typing in the numbers.

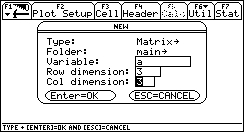
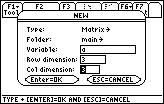
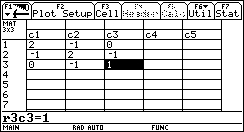
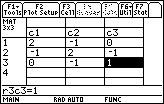
5. After we have completed the matrix as shown above, we will now return to the HOME screen. All the commands we need must be accessed from the HOME screen. Press the HOME button on the TI-89, or Diamond+Q on the TI-92(+).

Our matrix is now ready for use, and is stored as a variable called "a" in our MAIN folder.
Step 2: Finding the Eigenvalues of a matrix.

? How do I "tell" the calculator I want to do something with a variable (or an expression)?

Ans The question is: how does the calculator accept our requests? Well, the idea is simple: the calculator comes with built-in functions. A function recieves a variable or an expression, and returns the result of the specific operation(s) that it does. All results are returned to the HOME screen.

? How do I know which function I need to call?

Ans All the built-in functions are documented in the manual. You can read about what types of input the functions recieve; the operation they do on it, and the result they return.

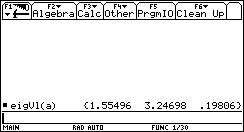
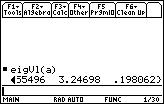
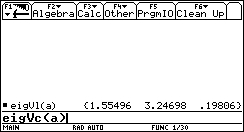
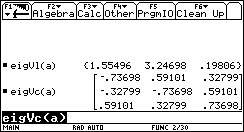
1. The function we need is called: eigVl.

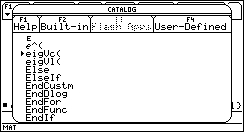
There's no need to type it in letter by letter -- the function names are easily found in the CATALOG. Press the CATALOG key on the TI-89, or 2nd+2 on the TI-92.

2. We can quickly "jump" to the functions beginning with the letter "e" by pressing the button that types the "e" letter: ÷ (the divide by key). (TI-89 users: Don't press or hold the alpha key first -- you are already in alpha mode. Check the alpha indicator!)

If you haven't already done so, Press the "e" key to "jump" through the CATALOG.

3. Use the arrow keys to scroll down to eigVl( , then hit ENTER. The command's (function's) name is pasted on the HOME screen.
4. Complete the command by typing the variable's name the function will receive: "a" and closing the parenthesis.
5. Press the ENTER key. The fnctions eigVl will run using the variable "a" as input. The result will be the eigenvalues of the matrix contained in "a":
6. On the TI-89: Scroll up once, and then sideways to see the full answer.
These are the three eigenvalues of our matrix.
Step 3: Finding the Eigenvectors of a matrix

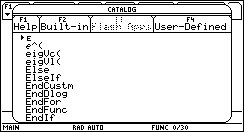
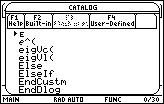
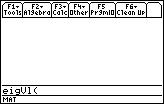
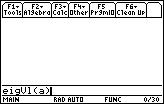
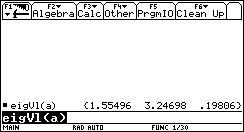
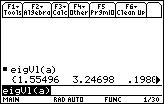
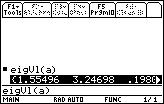
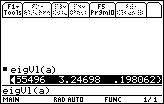
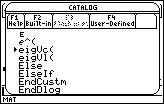
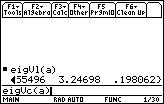
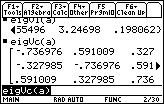
The function that returns the eigenvectors of a matrix is eigVc.

1. Return to the Entry Line by scrolling down. Clear the Entry Line by pressing the CLEAR button.
2. Press CATALOG and scroll to eigVc(.
3. Just as before, Press ENTER to paste the command on the Entry Line and complete the command by adding the variable's name "a" and a closing paranthesis.
4. Hit ENTER and the function will return the eigenvectors of the matrix, in the same order as its eigenvalues. i.e., the first column corresponds to the first (leftmost) eigenvalue.
5. TI-89 users: Use the arrow keys again to scroll up once and sideways and examine the result.
Congratulations! You have completed this task!

______________________________________________________________________________________

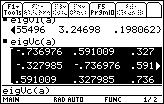
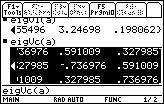
Created by Andrew Cacovean, Aug. 8, 2000