Solving Equations
Checklist: 
- is your calculator on?
- are you on the HOME screen?
- is the cursor on the Entry Line?
- is the Entry Line empty?
Suppose the analysis of a thermodynamic system containing ideal gas requires the solution of Van der Waals' equation for volume,
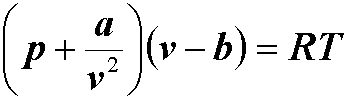
for CO2 at 200 F and 1000 psia. What this literally means is that in our equation
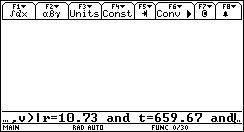
R= 10.73 [psia ft^3/lbmole R]
T= 659.67 [R]
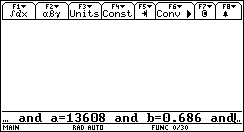
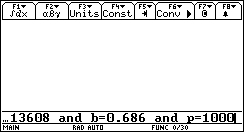
a= 13608 [psi ft^6/ lbmole^2]
b= 0.686 [ft^3/lbmole]
p= 1000 [psia]
and we are solving for v.
If we were solving by hand, we would have done the following:
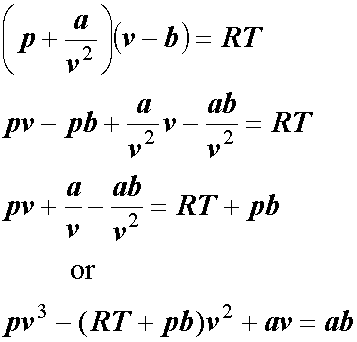
The equation is a third order polynom. The easiest method to solve for v would then be using Newton-Raphson's iterations etc. None of this is necessary with the TIs ,and indeed with any recent graphic calculator (including HP's). How do we solve this equation for v on the TI89 or TI92(+)?
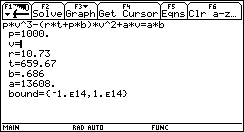
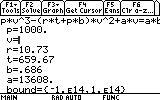
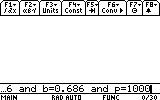
The answer is simple: let's think of how we would phrase our problem in human language. We would probably say something like: "We need to solve this equation for v when R=10.73, T=659.67, a=13608, b=0.686 and p=1000."
Well then -- that's exactly what we will tell the calculator to do!
1. We need to solve(...
(CATALOG on the TI-89/ 2nd+2 on the TI-92(+), "s", scroll down to "solve(" , ENTER)
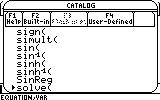
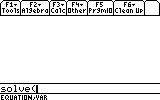
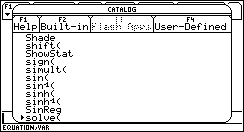

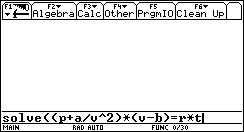
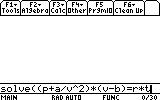
2. ... this equation...
(type in the equation)
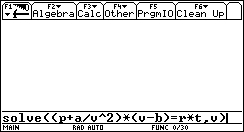
3. ... for v...
(add ",v" and close the parentheses)

4. ... when R=10.73, T=659.67, a=13608, b=0.686 and p=1000.
(the commas mean that we are actually saying that R=10.73 and T=659.67 and a=13608 etc. and this exactly what we tell the calculator)
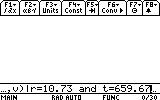

? Why the "|" sign? What does it mean?
Ans The "|" sign is the when (or with) operator. After writing the call to a function just as we called the function solve here, we can use this sign to add information necessary to process the command. Here I chose to include the information for R, T, a, b and p right after the command, so that it would all fit into one line and save entries. This way it would also be easy to edit the assignments we made. Adding information does not create any of the mentioned variables and will replace (not overwrite) the contents of existing ones.
Instead of adding this information after the command, we could actually create the information by letting "10.73->R", "659.57->T" etc. just as we define any other variable. However, this takes up more lines, and makes it harder to remember what each variable's value is exactly at the moment of solution, which could result in an incorrect answer.
Sometimes using this operator is necessary for solution. The identity
ln(x)+ln(y)=ln(x*y)
is correct (in real numbers only) when x>0 and y>0. The CAS, which is the operating system the TI89 and TI92(+) work with, will therefore not simplify the LHS of the identity into its RHS, without adding the information that x>0 and y>0. Other more important cases when the CAS will complicate the calculation if not provided with such additional information are common when differentiating certain functions, but we will not elaborate on this subject further.


? Where are the other two solutions (to the third order polynom)?
Ans Good question. In fact, this is a state equation, and therefore is single valued ( 1-1 ), just like plain old pV=RT. There simply cannot be more than one solution to the specific physical system.
Nevertheless, solving for a polynom will usually return an answer of the form x=x1 or x=x2 or x=x3 etc.
Why did we use the solve function to find v? We could have, as mentioned earlier, used the third order polynom with Newton-Raphson's iterations (simplest). We could have drawn a table, derive the polynom, draw up a table and start punching numbers.
But is there a better way? Yes, there is! The TIs all have a Numeric Solver. It does all the iterations by itself! In this task, we will take the polynom and solve it instead of the Van der Waals' equation, in four easy steps.
? Why the polynom and not the original equation? Can't the Numeric Solver solve the original?
Ans Of course it can. But I thought a little diversity wouldn't hurt. The following can be done just as easily for the original equation.
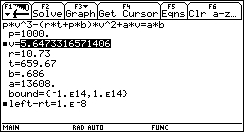
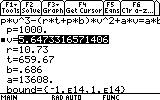
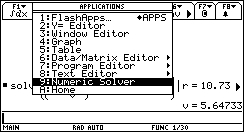
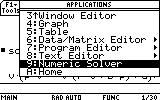
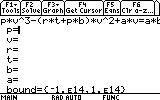
1. Open the Numeric Solver by pressing the APPS button, and scrolling down to Numeric Solver and pressing ENTER.
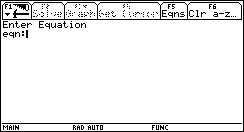
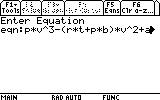
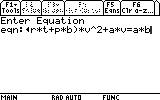
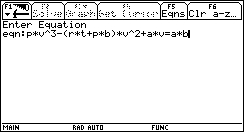
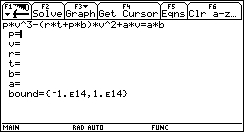
? What if I have an equation where I don't know an unknown's value beside the one I'm solving for?
Ans Then you can't use the Numeric Solver. Use solve instead.
R= 10.73, T= 659.67, a= 13608, b= 0.686, p= 1000
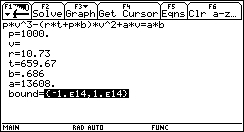
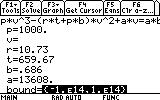
? What's a "bound"?
Ans Simple -- the range of numbers within which the Numeric Solver will search for the solution. Those familiar with Numerical Analysis methods know that there are certain pathological cases when the method cannot converge to the desired solution, but insists on converging to another. In these cases ristricting the search bound will help find the desired solution. In other cases a method could diverge at a singular point, making it imposible to find the solution. Restricting the bound in such cases, so that the singular point is excluded, will help the method to converge. Further discussion may be found in numerical recipes or numerical analysis theory books. Those not familiar with the above problems shouldn't worry -- the problematic equations are not so common, and more advanced methods than Newton-Raphson's do not fail so often.
? What about "v="? What should I write there?
Ans To complete the previous answer, it is possible to provide an initial guess other than the default (which is BTW not mentioned in the handbook but I suppose it's the mid point between the given boundaries). This is done by entering a number at the "v=" line. This is not neccessary here.