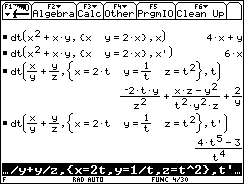
dt(ContinuousFunc,{IndependantFunc1,IndependantFunc2,...},IndependantVar)
ContinuousFunc: A function of one or more functions or variables.
IndependantFunc: The variable or function definition. Do not enter x=x, y=y, etc., for any expression. If a variable does not represent an independant function then list only the variable (see x in example 2). If x=x (etc.) is used, it will evaluate to "true" and the function can not tell which variable is being used.
IndependantVar: The variable to differentiate with respect to.
If this variable is postfixed with the prime symbol ('), the returned expression
will be in terms of IndependantVar, otherwise it will be in terms
of the IndependantFunc's (see examples). The prime symbol is [2nd][b]
on the TI-92 and [2nd][=] on the TI-89.
Return value:
This function returns the total derivative, also known as the Chain
Rule.
Examples:
1. If u=x/y+y/z, and
if x=2t, y=1/t, z=t2, the total derivative of u is
a. dt(x/y+y/z,{x=2t,y=1/t,z=t2},t)
[in terms of the IndependantFunc's x, y, z]
=
-2ty/z2+(xz-y2)/(t2y2z)+2/y
b.
dt(x/y+y/z,{x=2t,y=1/t,z=t2},t') [in terms
of the IndependantVar (t')]
=
(4t5-3)/t4
2. If u=x2+xy, and if y=2x, then
a. dt(x2+xy,{x,y=2x},x)
[in terms of the IndependantFunc's x, y]
= 4x+y
b. dt(x2+xy,{x,y=2x},x')
[in terms of the IndependantVar (x')]
= 6x