PDERelax BETA 0.14

Numerical Partial Differential Equation solver

Author: Bhuvanesh Bhatt (bbhatt1@towson.edu)

Description:
PDERelax is a Partial Differential Equation solver.

It currently solves the Poisson equation (negative sign and constant incorporated into source function):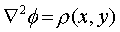

numerically on a grid. It is the only PDE solver written for a calculator.

Known problems:

There are no known problems. If you encounter one, please e-mail me.

What's new in BETA 0.14:

· PDERelax now solves the Poisson equation

· The feedback mechanism (during the calculation) has been changed (now the root-mean-square Laplacian and the number of iterations are shown)

· Crash with matrices larger than 19*19 has been fixed, with E.W.'s help

Syntax: PDERelax(guessMatrix,boundaryMatrix[,sourceMatrix[,maxiter[,eps]]])

PDERelax() shows a help message in the status line.

Requirements:

All arguments must be numeric (no symbolic values allowed), although exact numeric values are allowed.

Arguments:

· guessMatrix is an initial guess for the potential. It also specifies boundary values of the potential.

· The elements of boundaryMatrix should be 1 or 0, specifying whether the points lie or do not lie on the boundary. The potential does not change for boundary points, so choose the initial guess for boundary points carefully. boundaryMatrix should, of course, have the same dimensions as guessMatrix. The boundary surfaces should be parallel to the coordinate axes. As far as I know, the program works best for square matrices, although non-square matrices are allowed.

· sourceMatrix is the rho(x,y) from the right-hand side of the Poisson equation. If a source matrix is not entered, PDERelax solves the Laplace equation.

· maxiter = maximum number of iterations (default 100 iterations)

· eps = tolerance (default tolerance 1*10^-6)

Hints:

To get a good representative solution, try to strike a good balance between grid size and using the grid to represent the boundary geometry as well as possible (ideally, the boundaries should lie along the grid points, but this is not always practically possible). Larger grids take up more memory and take more time to converge. If you have curved or slanted boundaries, try to approximate them by rectilinear paths on as fine a grid as possible. As far as I can tell, the maximum (square) grid size is 126*126, because of the limit on the size of variables (the AMS allows creation of matrices with size only up to 32k).

Examples:

[0, 0, 0, 0, 0;
0, 0.01, 0, 0.01, 0;
0, 0, 0.005, 0, 0;
0, 0.01, 0, 0.01, 0;
0, 0, 0, 0, 0]®mat1

[0, 0, 0, 0, 0;
0, 1, 0, 1, 0;
0, 0, 0, 0, 0;
0, 1, 0, 1, 0;
0, 0, 0, 0, 0]®mat2

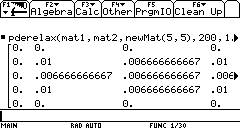
PDERelax(mat1,mat2,newmat(5,5),150,1E-8) returns the solution matrix:

[[0., 0., 0., 0., 0.]

[0., 0.01, 0.006666710021, 0.01, 0.]

[0., 0.006666710021, 0.006666844321, 0.006666710021, 0.]

[0., 0.01, 0.006666710021, 0.01, 0.]

[0., 0., 0., 0., 0.]]

As you make more iterations, the 0.006666... values will approach 2/300.

This was just a "toy" example, just to get a feel for the program. Let's move to a larger, more realistic example:

rho(x,y) = when(x=0 and y=0,1,0)

boundary(x,y) = 0 at the edges of the grid

This corresponds to a point charge in the center.

We generate the matrices:

seq(seq(when(i=20 and j=20,1,0),j,1,39),i,1,39)->src

newMat(39,39)->guess

seq(seq(when(i=1 or j=1 or i=39 or j=39,1,0),j,1,39),i,1,39)->bnd

PDERelax(guess,bnd,src,250,1E-3) //This takes about 5min 40sec

Visualizing the resulting matrix would be nice, but one step at a time :-)

Please let me know of your opinions about this program, including design issues such as syntax.

Future plans:

I would like to make this into a fully-featured PDE solver that solves all or most common PDEs (including nonlinear ones) from mathematical physics. To achieve this, the syntax may change. I am still learning about the various techniques for solving PDEs, so this project will probably take a while.

Disclaimer:

This is a beta version and has not been tested for

either stability or accuracy. It may crash or hang.

I am not responsible for any damage done to your

calculator. To reset the calculator, press:

[2nd][LOCK][ON] on the TI-92 Plus

[2nd][LEFT][RIGHT][ON] on the TI-89

If this doesn't reset the calculator, take out

a battery, press and hold [(-)][)] while you insert

the battery.

Of course, this does not mean your calculator will

definitely crash or hang :) In fact, you should be

able to break a calculation by pressing [ON].

Copyright Bhuvanesh Bhatt.