Polynomial algebra:

 

§         Coefficients and terms

§         Polynomial division

§         Resultants

§         Factorization

§         Gröbner bases

§         Other functions

 

 

w        Coefficients and terms

§         Coef(poly,x) returns the coefficients of poly in the variable x
Example: Coef(x3-6×x2+11×x-6,x) Ž {1,-6,11,-6}
Note: The exponents must be numeric (for example, x2 is valid but xa is not).

§         CoefList(poly,x) is an alternative function for returning the coefficients of poly
Needs: FreeQ, IsCmplxN, Pad, PolyDeg
Examples: CoefList((a+b×i)×x3+(c+d×i)×x+(e+f×i),x) Ž {e+f×i,c+d×i,0,a+b×i}
Note: This function is experimental and slow, and may return incorrect results.

§         Degree(poly,x) returns the degree of poly in x
Needs: Coef
Example: Degree(x2-x+1,x) Ž 2

§         LeadCoef(poly,x) returns the leading coefficient of poly in x
Needs: Coef
Example: LeadCoef((x+x)(x+2×x2)(x+3×x3),x) Ž 12

§         LeadTerm(poly) returns the leading term in poly
Example: LeadTerm(4×x×y×z2+4×x3-5×y4+7×x×y2×z) Ž 4×x3

§         NthCoeff(poly,x,n) returns the coefficient of xn in poly
Examples: seq(NthCoeff(x3-x+1,x,i),i,4,0,-1) Ž {0,1,0,-1,1},
                  seq(NthCoeff(-@n12+Ö(a)×@n1+eb,@n1,i),i,3,0,-1) Ž {0,-1,Ö(a),eb},
                  NthCoeff(-3×x100+2×x4-7,x,100) Ž -3
Note: NthCoeff can handle polynomials with degrees upto 449.

§         PolyDeg(poly,x) is an alternative function that returns the degree of poly in x
Needs: MatchQ
Example: PolyDeg(-5×x4-x2+4×x-5,x) Ž 4

§         sFactors(xpr) returns a list of all symbolic factors in xpr
Needs: nChars
Example: sFactors((x+1)×(x-2)) Ž {x-2, x+1}
Note: sFactors is very similar to Terms, except that it deals with multiplication instead of addition. If xpr is provided as a string, the factors are found without any evaluation.

§         Terms(xpr) returns a list of terms in xpr
Needs: nChars
Example: Terms(cos(a+b)×x2+e2×c×x) Ž {cos(a+b)×x2, (ec)2×x}
Note: If xpr is provided as a string, the terms are found without any evaluation.

w        Polynomial division

§         ExtGCD(poly1,poly2) returns polynomials {d,{s,t}} such that
d = s×poly1+t×poly2 = GCD(poly1,poly2)
Needs: IsCmplxN, Quotient, VarList
Example: ExtGCD(5×x2+x-4, x2-1) Ž {d = x+1, st = {1, -5}}
Note: ExtGCD also works for integers. The extended gcd is useful for solving linear Diophantine equations.

§         MPolyDiv(poly1,poly2,x) returns polynomial quotient and remainder for multivariate polynomials
Needs: LeadTerm, Remaindr
Example: MPolyDiv(x2-y,x+y,{x,y}) Ž {x-y,y2-y}

§         PolyDiv(poly1,poly2,x) returns the univariate polynomial quotient and remainder
Needs: Coef, Degree, LeadCoef
Example: PolyDiv(3×x4+2×x3+x+5,x2+2×x+3,x) Ž {3×x2-4×x-1,15×x+8}

§         PolyGCD(poly1,poly2,x) returns the polynomial GCD of poly1 and poly2
Needs: Coef, PrimPoly, Remaindr
Example: PolyGCD(12×x3-28×x2+20×x-4,-12×x2+10×x-2,x) Ž 3×x-1
Note: Intermediate expression swell is encountered in polynomial gcd computation, especially with the classical Euclidean algorithm.

§         PolyLCM(poly1,poly2,x) returns the polynomial LCM of poly1 and poly2
Needs: PolyGCD
Example: PolyLCM((1-x)2×(1+x)2,(1-x)×(2+x),x) Ž (x-1)2×(x+1)2×(x+2)

§         Quotient(poly1,poly2,x) returns PolyDiv[1] (polynomial quotient)
Needs: PolyDiv
Example: Quotient(3×x4+2×x3+x+5,x2+2×x+3,x) Ž 3×x2-4×x-1

§         Remaindr(poly1,poly2,x) returns PolyDiv[2] (polynomial remainder)
Needs: PolyDiv
Example: Remaindr(3×x4+2×x3+x+5,x2+2×x+3,x) Ž 15×x+8

w        Resultants

§         Resultnt(poly1,poly2,x) returns the polynomial resultant
Needs: Sylvestr
Example: Resultnt(x2-2,x3-1,x) Ž -7

§         Subres(poly1,poly2,x) returns a list of polynomial subresultants
Needs: Coef
Example: Subres(2×x4+x2-4,3×x2+2,x) Ž {1156,102}

§         Sylvestr(poly1,poly2,x) returns the Sylvester matrix
Needs: Coef
Example: Sylvestr(x2-3×x,x3-1,x)
                Ž [[1,0,0,1,0][-3,1,0,0,1][0,-3,1,0,0][0,0,-3,-1,0][0,0,0,0,-1]]
Note: Sylvestr cannot handle constant (degree 0) polynomials.

w        Factorization

§         BerlQMat(poly,x,m) returns the Berlekamp Q-matrix modulo m
Needs: Coef, Reverse, sMod
Example: BerlQMat(x2+3×x,x,2) Ž [[1,0,0][0,1,0][0,1,0]]
Note: Finding the null-space of the Q-matrix modulo a prime is a first step in the Berlekamp factorization algorithm.

§         SqFree(poly,x) finds the squarefree factorization for a primitive polynomial poly
Needs: PolyGCD
Example: SqFree(x3+5×x2+8×x+4,x) Ž (x+1)×(x+2)2
Note: Squarefree factorization is a first step in many factoring algorithms. There is a Flash app extension function MathTool.SqrFree that does the same thing as SqFree, but faster.
Note: SqFree finds the derivative of poly and then iteratively computes GCDs.

§         SqFreeQ(poly,x) returns true if poly is squarefree, else false
Needs: PolyGCD
Examples: SqFreeQ(x5+x3+2×x2+x+2,x) Ž true
                  SqFreeQ(x8-2×x6+2×x2-1,x) Ž false

w        Gröbner bases

§         Groebner(polylist,vars) computes a symbolic Gröbner basis for the set of multivariate polynomials in polylist
Needs: ListPair, NormalF, Spoly
Example: Groebner({x-y-z,x+y-z2,x2+y2-1},{x,y,z}) [will take »30 minutes!]
Notes: Groebner is a program, unlike most other components of this package.  It is an experimental program and is usually very slow. Groebner computes the (unreduced) Gröbner basis via the Buchberger algorithm. At each step, it shows the combination of polynomials selected ({ pi , pj }) and the normal form of Spoly(pi , pj). Computing a symbolic Gröbner basis with a lexicographic ordering can be computationally intensive. When Groebner ends, it displays the Gröbner basis. Gröbner bases can be used to solve systems of polynomial equations, and are also useful for other applications such as integer programming and converting parametric curves and surfaces to implicit form. The reduced Gröbner basis has the same set of roots as the original polynomials. If the Gröbner basis reduces to 1, the nonlinear system polylist has no solution.

§         NormalF(poly,polylist,vars) returns the normal form of poly modulo polylist
Needs: LeadTerm, MPolyDiv, Terms
Example: NormalF(x+y-z2,x-y-z,{x,y,z}) Ž 2×y-z2+z
Note: The “normal form” is guaranteed to be unique only if the polynomials in polylist form a Gröbner basis.

§         Spoly(poly1,poly2,vars) returns the S-polynomial of poly1 and poly2
Needs: LeadTerm, Multideg
Example: Spoly(x3-2×x×y,x2×y-2×y2+x,{x,y}) Ž -x2

w        Other functions

§         CompMat(poly,x) returns the companion matrix of poly
Needs: Degree, Reverse
Example: CompMat(x2+1,x) Ž [[0,-1][1,0]], eigVl([[0,-1][1,0]]) Ž {i, -i}
Note: The eigenvalues of the companion matrix are the roots of poly, as demonstrated in the example above.

§         Content(poly,x) returns the “content” of poly
Needs: Coef, LGcd
Example: Content(8×x4-2×x2-2×x+12,x) Ž 2
Note: The “content” of a polynomial is the gcd of its coefficients.

§         Cyclotom(n,x) returns the nth cyclotomic polynomial
Needs: RelPrime
Example: Cyclotom(6,x) Ž x2-x+1
Note: The nth cyclotomic polynomial is the minimal polynomial of the primitive nth root of unity and is irreducible over Integers with degree j(n), where j(n) is the Euler totient function.

§         mMinPoly(mat,var) returns the minimal polynomial of mat in terms of var
Needs: NullVecs
Examples: mMinPoly([[0,0][0,0]],x) Ž x, mMinPoly([[0,1][0,0]],x) Ž x2,
                  mMinPoly([[1,0][0,1]],x) Ž x-1
Note: The minimal polynomial of a matrix M is the lowest degree polynomial such that 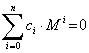, where n is the polynomial degree. It divides the characteristic polynomial of M.

§         Multideg(poly,vars) returns the multidegree of poly
Needs: Degree, LeadTerm
Example: Multideg(4×x×y×z2+4×x3-5×y4+7×x×y2×z,{x,y,z}) Ž {3,0,0}

§         Normal(poly,x) returns the normal form of poly
Needs: LeadCoef
Example: expand(Normal(8×x4-2×x2-2×x+12,x)) Ž x4-x2/4-x/4+3/2
Note: This is not the same normal form as that given by NormalF.

§         PolyMod(poly,m,x) returns poly mod m
Needs: Coef, IsCmplxN, Quotient
Example: PolyMod(x6+6×x5+15×x4+20×x3+15×x2+6×x+1,2,x) Ž x6+x4+x2+1

§         PolyQ(xpr,x) returns true if xpr is a polynomial, else false
Example: PolyQ((x+1)2, x) Ž true
Note: If you have variables raised to unknown powers, PolyQ will return false. For example, PolyQ(x2×yb,x) Ž false

§         PrimPoly(poly,x) returns the corresponding primitive polynomial
Needs: Content
Example: PrimPoly(6×x3+26×x2+26×x+6,x) Ž 3×x3+13×x2+13×x+3

§         SymPoly(list,k) returns the kth symmetric polynomial of the variables in list
Needs: KSubsets
Example: seq(SymPoly({x,y,z},i),i,1,3) Ž {x+y+z, x×y+x×z+y×z, x×y×z}

 

 

MathTools and its documentation copyright Ó Bhuvanesh Bhatt (bbhatt1@towson.edu)