![[Some graphics I lifted from TI's website.]](3ticalcs.gif){kind=small}
Top of FAQDisregarding the 73 because it's a junior high school level calculator, there are three model families of graphing calculator made by TI: the TI-83 family, the TI-85/86, and the TI-89 family. Between the three families they all take similar effort to learn for the new user, changing from one to another can cause brief confusion. (TI has a web page to ease the transition up to the 89 family from the 8x calculators.)
The 83 family is TI's flagship model family for high school level math. It's used by most teachers in the classroom, allowing students with the same thing to follow along without having learned to use the calculator by reading the manual. (Though reading the manual is still a good idea.) It possesses all the standard functions needed for math curriculums up to and including calculus. The TI-84 Plus Silver Edition is the best model of the 83 family.
The TI-86 has many useful functions that are not built in to the 83 family calculators, though
most of them are available for the 83+/84+ as Flash applications. It includes everything the 83
family has except for built-in sequence graphing, finance functions, and advanced statistics
functions, though the latter two are available for the 86 as free add-on programs from TI. The 86
does lack Flash ROM, but Flash ROM is far from a vital feature, especially since it has so many
more features already built in. The 86 is a better calculator than the 83 family overall, with
definite advantages in calculus and science functions. However, it's all but faded away in favor of
the 89, even though the 89's far superior power is inappropriate for math before calculus. On the
pro side, the 86 (and the 83 family for that matter) seems to be slightly better than the 89 for plain
and simple number crunching since it doesn't have the symbolic manipulation to worry about. It's
an excellent choice for people who find that the 89 family is too much but the 83 family is not enough.
Note: If you do buy an 86, be aware that most teachers have been trained on the 83 family and
won't be familiar enough with the 86's interface to help you use it. The commands themselves are
almost all the same, but the menus are arranged differently. Be sure to read or at least skim your
86 manual to familiarize yourself with its menus and mode/format screens.
The TI-85 is only a small step below the 86 in functionality. It is no longer manufactured.
The 89 family is the highest level calculator TI makes with advanced abilities including 3-D graphing, symbolic manipulation, and CAS. Such features are not needed for high school level math. (If algebra was a small nail, the 89 family would be a sledgehammer.) However, if you plan to continue on to college level math, it is not an altogether bad thing to have an 89 family calculator as early as calculus. It is especially useful in higher level calculus classes and beyond, and for engineers. The TI-89 Titanium and Voyage 200 are the best models of the 89 family, both possessing the same software and functionality. The Voyage 200 and 92(Plus) are not allowed for standardized tests on account of the qwerty keyboard. Additionally, the 89(Ti) is banned by the ACT due to its CAS abilities.
When in doubt, ask your teacher or your school's math department which calculator you should get. This can even be a necessity in some cases where the school or teacher is aware of the 89 family's CAS power and does not allow it in certain classes, or if they make extensive use of the calculator's data transfer ability in which case it's essential to have a proper model.
TI's calculator comparison chart![[PDF file]](pdf.gif){kind=small}
better shows what each calculator can and
can't do.
Get second opinions from ticalc.org, Ron Ross, or Business Week.
The various incarnations of the TI-83 can be confusing. Here's a breakdown of the 83 family in chronological order of release:
The TI-84 Plus Silver Edition is the best choice of these. If you already own an earlier model however, it's still similar enough that there shouldn't be a need to upgrade to the TI-84 Plus Silver Edition.
The various incarnations of the TI-89 can be confusing. It's also known as the 68k family after the 68000 CPU used in them. Here's a breakdown of the 89 family in chronological order of release:
The TI-89 Titanium and Voyage 200 are the best in this family, choose between them depending on if you want the qwerty keyboard and larger screen or not. If you already own an earlier model however, it's still similar enough that there shouldn't be a need to upgrade to the TI-89 Titanium or Voyage 200.
TI's first graphing calculator was the underpowered (by today's standards) TI-81. The next entry was the well-rounded TI-85, which had quite a bit of functionality and IMO an absolutely marvelous menu system. Presumably, TI started soliciting teachers for their opinion of the TI-85 and the word came back that the TI-85 had too much functionality, things that would not be used by the teachers and which would be potentially confusing to the students. So TI took the TI-85 back to the shop and cleared out many of the truly useful things, including long variable names and imaginary numbers. While they were at it, they did come up with some new things, like the Text() command and the Table function. With the TI-82 that resulted, TI began their marketing effort in earnest, and pretty soon teachers across the nation were using the TI-82 in class and making their students buy them too.
The TI-85 still had a main advantage in some calculus functions that the TI-82 didn't have, but that ended when the TI-92 came out. Since the TI-92 had a CAS, it far outclassed the TI-85 and became as popular with calculus teachers as the TI-82 was with algebra teachers. The TI-85, already a minority due to the lack of marketing effort behind it, now became completely marginalized due to the two-tiered system of the TI-82 and TI-92 which were endorsed for student use by TI and teachers. Given low-end and high-end calculators, there is no place for the middle-end model. Somewhere around this time TI also put out the TI-80, which was very similar to the TI-81 and just as memorable, i.e. not at all.
At this point TI had covered all the levels of mathematics education they needed to and went back to improve what they already had. The big selling TI-82 became the TI-83 along with some new features like graph styles and financial functions. Imaginary numbers went back in too, though it still lacked most of the things that made the TI-85 a far better calculator. The TI-85 itself had enough of a following left from the pre-TI-82 days to warrant its own upgrade to the TI-86, which combined all the TI-85 had to offer with the small amount of nifty new things TI had introduced with the TI-82 and TI-83, along with a sizable memory upgrade. Of course it still couldn't make any headway against the two-tiered system of the TI-83 and TI-92, and TI has been more or less ignoring the TI-85/86 model family ever since, looking back only long enough to stop production on the TI-85.
TI's next big idea was the use of Flash ROM, and the proof of concept took advantage of the expansion slot they'd built into the TI-92 in the form of the Plus Module. It worked fairly well, and they went ahead with the TI-73, an underwhelming middle school/junior high level calculator that never caught on, and another version of the big seller, now called the TI-83 Plus. The Flash enabled TI-92 with Plus Module was reworked into the TI-89 for those who where sick of the brick-like TI-92, and a TI-92 Plus proper was also released.
Flash Applications became abundant. Most of the features that the TI-86 has and the TI-83 doesn't turned up as Flash Applications for the TI-83 Plus. If one doesn't mind loading up the Flash ROM space, the TI-83 Plus can have everything it lacks except long variable names. The TI-86's extremely useful polynomial solver and simultaneous equation solver turned up as Flash Applications for the 89 family as well, although in that cases it was only a cosmetic improvement, as that calculator could already handle such problems using native functions.
Next in line as a marginal improvements to the TI-83 model family was the TI-83 Plus Silver Edition, adding a massive amount of Flash ROM archive space, a suite of preloaded Flash Applications, a faster processor, and a black serial TI Conenctivty cable included in the package (later superseded by the silver USB Connectivity cable). They billed it as being for "power users". This of course ignoring the facts that the true "power users" of the TI user community all own the TI-89 or TI-92 Plus, and that even a power user with a TI-83 series calculator is mostly outclassed by the forgotten TI-86. The follow-up to the 92 Plus was the Voyage 200, which thankfully reduced the case size, and added more Flash ROM, preloaded Flash Applications, and an included USB Connectivity cable. The 89 later got the same treatment and became the 89 Titanium.
A passing fad with TI's marketing department was for the calculators to be claimed as useful in classes other than math and science, as demonstrated by the Study Cards Flash Application and the Voyage 200's original "Personal Learning Tool" moniker. (Even though a calculator being useful outside of math and science is more or less an oxymoron.) This was perhaps to combat vocal attempts by Palm Pilot to get their PDA used in classrooms. TI projected the image of the Voyage 200 as an educational PDA of sorts, even though it's essentially identical to the TI-92 Plus.
With the calculators so ingrained into math classrooms, to the point that handouts and whole textbooks revolve around them, it became vital that newly released calculators function exactly as their predecessors had, button by button and menu by menu. This led to the odd juxtaposition that the primary feature of each new calculator is that it has no new features to speak of. Though this was evident as early as the TI-83 Plus, it was driven home by the next updates to the 83 family, the simultaneously released TI-84 Plus and TI-84 Plus Silver Edition. The only improvements above the TI-83 Plus Silver Edition they had to boast about were ViewScreen ports on every calculator (a feature formerly found only on specially made versions) and mini USB link ports, along with the laughable changeable faceplate given to the TI-84 Plus Silver Edition.
Compared to the early days, TI has taken strides in recognizing the existence of calculator games and the significant presence of TI graphing calculator users on the internet. Highlighted as a preloaded Flash Application on the TI-83 Plus Silver Edition was Detached Solutions' game collection PuzzPack. TI worked with ticalc.org to make a CD-ROM of popular games from their program archive for inclusion in Connectivity kit packages, although that ended in disaster. When the TI website was revamped to include a flashy student section, it included a games page with featured games and links to several of the best known calculator related websites.
ticalc.org's calculator list page
Read about the competitors on this page.
New: TI keeps a list of stores that sell their calculators. Some of them even have on-line purchasing. The Instructional Dealers sometimes sell for slightly less than the retail prices. For outside of North America, go to TI's International Information page. TI's online store sells calculators and Connectivity cables as well.
Remanufactured: According to a post several years ago by a fellow named Helpful in TI's discussion groups, remanufactured calculators (returned to the store as defective and repaired by TI) are sold at a discount by the Bach Company in Palo Alto, CA. Bach's phone number is 1-650-424-0800.
Used: TI has banned solicitation of calculators on their discussion groups (due to some legal issue, I imagine). UsedCalculators.com, as the name implies, sells used calculators but their prices aren't a whole lot better than buying new. You can also find used and new calculators on eBay and other auction sites.
You can buy manuals and calc to calc link cables from TI, call 1-800-TI-CARES or visit TI's on-line store. TI also has all of the calculator manuals available as Adobe Acrobat (.pdf) files, including the full version of the manuals for those who find the mini-manual that comes with the calculator to be deficient. Many people find the manual too hard to understand. They also keep a list of other books about using their calculators. These books can be bought from TI or from the Instructional Dealers, and selected chapters can be read online at TI's website. Of course, books for one calculator also apply for the most part to the other calculators in the same model family (i.e. TI-82/83(+[SE])/84+[SE], TI-85/86, TI-89(Ti)/92(+)/V200).
And yes, they do have "...for Dummies" books for the TI-83 Plus and TI-84 Plus. Also available is a TI-83 Plus Engineering Applications Handbook.
TI's list of tutorials - Covering the 83 family, the 89 family, and more.
TI's KnowledgeBase - Searchable database of FAQs and instructions.
TI's TI-89 Tips for the TI-83 User
Hanover High School's TI Graphing Calculator Help - 83+
Mathbits.com's Finding Your Way Around the TI-83+/TI-84+ Graphing Calculator - 83 family
MSU-Billings Academic Support Center - 83+, 85/86, and 89/92, includes videos.
Prentice Hall - Shows keystrokes for common tasks on all graphing calculators.
Prof. Quagliato's TI-92 tutorial.
RIT Calculator Resource Site - Calculus tutorials for all graphing calculators.
Titutorials.com - for the 83(+), but this one isn't free.
89/92+ Examples - for the 89 Flash family
WatchMe Ware - tutorial software for the 73, 83+, and 89. Free and priced versions.
William Larson's TI-89 and TI-83 Tips
Frank Wattenberg's TI-92 Help
Pythagoras Teachware - TI-89 family tutorials, with free sample pages
The ROM (Read Only Memory) contains the built-in software (Operating System) of the calculator. In the pre-Flash ROM days, as batches of calculators were manufactured, the ROM software was sometimes changed to reflect a bug fix or other minor improvement. Higher numbers are more recent versions. The difference between ROM versions is usually so small, it is often noticeable only to assembly program writers. (One of the few really noticeable changes was CBL compatibility that was added to the TI-85 with ROM version 9.0.) The TI-92 had upgradable ROM, as do the calculators with Flash ROM. (The current ROMs for flash calculators are available from TI's website. Old ROMs can be acquired by e-mailing TI, provided your e-mail provider can accept file attachments that large.) The ROM software of the TI-89 Flash family is called Advanced Mathematics Software or AMS. To get a new ROM version for the older non-Flash TI-8x calculators, you would have to buy an entire new calculator, and the difference isn't large enough to make that worth it.
About screen methods:
TI-83 Flash family: From the Memory menu (2nd-MEM) choose 1:About
TI-89 Flash family: From the home screen type F1, A
Self Test screen methods (Careful! Read about the self test first.):
TI-81: Go to the test screen and type Alpha S
TI-80, TI-8x: Go to the mode screen and type Alpha S
TI-92/TI-92 Plus/Voyage 200: From the home screen type F5, diamond, (
TI-89 AMS 1: From the home screen type F5, diamond, APPS
TI-89 AMS 2: From the home screen type F5, diamond, CLEAR
Note for the old 92: "Internal" ROM is part of the circuit board, and "External" ROM is a removable module. The Plus Module ROM upgrade will work with either.
When you are viewing the ROM version number of a TI-8x calculator, pressing enter will launch a self test which resets the calculator's memory. (So don't push enter unless you've got a backup.) Press any other button to leave the screen. From the 89 family's ROM version screen, the letter S accesses the self test menu where you can choose from several tests, and 2nd Quit leaves the screen. A word of warning though, if you look at the 89 family's self test menu screen, the bottom line of the entry area on the home screen will disappear. The only known way to get it back is to reset the memory. The Calc-TI FAQ describes the self test itself in more detail in section 2.4.
Buggy assembly programs and other random glitches can lock up calculators. The "Address Error" on the 89 family is one such lock up. If the screen won't come on, try turning up the contrast (2nd Up on the TI-8x, Diamond + on the 89 family). If the screen comes on dark, try turning the contrast down. Try a new set of batteries next, again remember to check the contrast. If that doesn't fix it or if it was locked up, you'll have to try a memory reset. Remove one battery and hold the ON button down for 10 seconds, then replace the battery.
If unsuccessful, remove all the batteries, including the lithium watch battery, and leave the calculator like that for several hours. (The back of the 89 family manual describes some key sequences for resetting as well: 2nd-hand-ON for the 92+/V200 and 2nd-left-right-ON for the 89(Ti). Other key combinations that may help get out of lock-ups are the negation sign and the closing parenthesis together, and Esc-On.) If it still doesn't work after you put the batteries back in and check the contrast, contact TI by e-mail or 1-800-TI-CARES and get their opinion.
If the screen comes on with an error message and does nothing but turn off again, read about reloading the OS.
If a calculator with Flash ROM displays a message such as "Press I to install code" (89 Flash family) or "Waiting...Please Install Calculator Software Now" (83 Flash family) and won't do anything else, it means the ROM was erased or corrupted and needs to be reflashed using TI Connect's OS Downloader and a ROM file from TI's website. Another calculator of the same model can also be used to reflash the ROM. The most common cause of this error is interruption of a flash upload, so make sure the batteries are fresh when you upload a ROM or flash application. If you continue to experience problems reflashing a ROM, call 1-800-TI-CARES.
TI-83 Plus note: Apparently the 83 Plus can display its "Please install calculator software now" message when the ROM is actually still present. There is no clear method to get the calculator to recognize the ROM again. One suggested remedy is to remove one battery, hold down the clear button while putting it back in, then press several buttons randomly until the OS comes back up with a Memory Cleared message. Another version says to turn the calculator on, then hit On, another button, On again, and then quickly press and hold Clear. A third reported instance involved turning the calculator on and off several times. The cause for this is unknown, but may be related to interference from assembly shells. Of course, actually reflashing the ROM will also solve the problem.
This is most often caused on the TI-83, TI-83 Flash family, and TI-86 when a plot is turned on without data in it. (For a valid plot, the lists that define it must be of equal non-zero length, otherwise the dimension error is given.) To correct the problem, simply turn off the plots in the y= screen or execute the PlotsOff command (PlOff on the 86). Another possible cause is invalid window settings, for instance if xMax is less than xMin. Activate one of the preset zoom settings to correct this.
Check your mode screen settings. The calculators default to radians, if you need to work in degrees you simply need to change the setting.
Also beware of graphing trig functions in degree mode unless you use ZoomTrig. If the window is set to the standard zoom of xMin=-10 and xMax=10, or anything close to that, you may only see a horizontal line. Actually, it's a good idea to use ZoomTrig when graphing a trig function in radian mode too.
If a TI-83 Flash family calculator will only allow one function on the Y= screen to be selected at a time, it is likely that the Transformation Graphing Flash Application has been activated. To turn it off and resume normal graphing conditions, go to the APPS menu and select Transfrm (or DemoTrns in the case of the App's demo version). A menu titled "TRANSFRM APP" should appear. Select 1:Uninstall from this menu to deactivate the App.
Things that the calculators can easily do but are not built in functions found in the manual.
This really is as simple as you might think. A mixed number such as 2¾ is merely a whole number added to a fraction, and a fraction is just the numerator divided by the denominator. So two and three fourths is typed 2+3/4. Don't forget to put the whole thing in parentheses if you're doing calculations with it.
To convert the displayed answers back into fraction form, see 11.1.4.
We all know about the reciprocal trigonometric functions,
1/sin x = csc x
1/cos x = sec x
1/tan x = cot x
and we all know how the calculator handles the inverse trigonometric functions,
sin-1 x = arcsin x
cos-1 x = arccos x
tan-1 x = arctan x
but how to do the inverse of the reciprocal functions? Well, here it is. I'll leave it to you to figure
out why this works since the math involved is pretty straightforward.
sin-1 (1/x) = arccsc x
cos-1 (1/x) = arcsec x
tan-1 (1/x) = arccot x
The csc, sec, cot, csc-1, sec-1, and cot-1 functions are included on the TI-89 Flash family in AMS 2.08 and above.
As any good math textbook will tell you, the logarithm change of base formula is:
logb a = log a/log b = ln a/ln b
Owners of the TI-89 family can even define a function
ln(a)/ln(b)
logb(a,b)
Kevin Kofler's XtraKeys program hacks the TI-89 Flash family so that a log base function is
available as an extra function of the ^ or ln key.
As any good math book will also tell you, the definition of the logarithm is:
log10 x = y when 10y = x
Therefore, the antilog is merely 10^.
Kevin Kofler's XtraKeys program hacks the TI-89 Flash family so that 10^ is available as an
extra function of the clear or home key.
There is no plus/minus sign on the calculators, but you can fake one. (The plus/minus sign is used
before a square root that was created to cancel out a square on the other side of the equation, for
instance when graphing a circle.) The list {1,-1} will multiply what follows it by one and
negative one. On the home screen, both results are returned in a list. In a graph, both results will
be graphed. For instance, to graph the circle x^2+y^2=16, enter y1={1,-1}
(16-x^2)
(The 89 family does have a plus/minus sign in the Char-Math menu, but it doesn't do much
functionally so the {1,-1} method is still more useful.)
To find the roots of an equation of the form A*x2+B*x+C=0
For the TI-83 family:
An example of typing the quadratic equation into the calculator is given in the Getting Started
chapter of the manual. For repeated use, it is simpler to turn it into a
program:
:Prompt A,B,C
:(-B+{1,-1}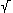(B2-4A*C))/(2A)L1
:Disp L1
Be sure to have the appropriate Mode setting on if you wish to see non-real answers.
There is a Polynomial Solver Flash Application for the TI-83 Flash family that functions much like the TI-86's polynomial solver.
For the TI-85/86:
The method from the TI-83 also works here, but the built in polynomial solver is much more
convenient. It is described in Chapter 15 of the TI-86 manual. To use it,
press 2nd-POLY and enter 2 for a quadratic since it is a second order polynomial. Then fill in the
coefficients of the quadratic, A for a2, B for a1, and C for a0. Press F5 to see the solutions.
For the TI-89 family:
Once again, writing the quadratic equation out will work, and there is a Polynomial Solver Flash
Application for the 89 Flash family as well, but this simple function can be used from the home
screen:
czeros(polyeval(list,x),x)
For a quadratic, it is entered as: poly({A,B,C})
If the Polynomial Solver Flash Application is installed, there will be a poly() command already
available. It works the same way as the constructed version I described.
Oddly enough, the calculators do this the same way as you write it on paper. For y1=f(x) and y2=g(x), f(g(x)) can be found using y1(y2(x)). (Only the TI-85 lacks the function notation necessary for this.) On the 89 family you can use any names you want for the functions, you are not limited to the graph equations. If you use the names f(x) and g(x), you can literally do f(g(x)), typing it in exactly like that.
Using matrices to solve a system of equations is an old standard in mathematics. This website explains how to do it on a TI calculator. (It's amazing what search engines will turn up when you use them.)
Also, the TI-89 Flash family can use the solve() command for a system of equations. The syntax, as seen in the manual, is solve(f(x,y) and g(x,y),{x,y}). A simultaneous equation solver is available as a Flash App for the TI-83 Flash family and the TI-89 Flash family, and is a built in feature of the TI-85/86.
You can store commonly used equations from the home screen for quick recall in the interactive numerical solver on the TI-85/86 (2nd-GRAPH) and the TI-89 Flash family ("Numeric Solver" in the APPS menu). As an example, I shall use two common science equations, but you don't have to know what they mean to understand the process.
My first example is kinetic energy equals one half mass times velocity squared, type it in like this
on the home screen:
TI-85/86: KE=.5M*V2
TI-89 Flash family: .5m*v^2ke
Start the solver. Along the bottom of the screen on the TI-85/86 is a list of all the equation
variables on the calculator. Press the F-key underneath KE and KE will appear on the eqn: line at
the top. On the TI-89 Flash family, type ke at the eqn: line. Now press enter, and solve away! Fill
in the known values, move the cursor to the unknown, and press the F-key for Solve. The
calculator will show exp= on the list of variables instead of KE=, but exp=KE is displayed at the
top so you won't forget what it means.
My second example is chemistry's universal gas law. This is useful when you want to have more
than one variable on each side of the equal sign. On the home screen, type:
TI-85/86: GASLAW=P*V=N*R*T
TI-89 Flash family: p*v=n*r*tgaslaw
Of course, you could have done P=N*R*T/V, but it's easier to identify the equation if it's named
Gaslaw instead of P. Start the solver. On the TI-85/86, hit RCL (2nd-STO>), then the F-key for
GASLAW, then ENTER. On the TI-89 Flash family, hit F1 then 1 (or diamond-o) and select
gaslaw from the dropdown list. This will put P*V=N*R*T as your equation, then press enter and
start solving.
(You could enter GASLAW as the eqn: directly, but then the calculator regards the equation as
GASLAW=P*V-(N*R*T). This will still work if you keep exp=0 (GASLAW=zero), but the
former method is a smidgen easier to use.)
The TI-83 and TI-83 Flash family has a similar solver, but instead of entering an equation you enter an expression that is equal to zero. This can be done by moving one side of the equation to the other using subtraction. (P*V=N*R*T becomes (P*V)-(N*R*T).) Equations can only be stored to the graph variables on the 83 family, which makes it impractical to store equations to use in the solver.
Data intended for regression is sometimes given in the form of calendar years. This can cause problems, especially for logistic regressions. It is best to treat the first year as year zero, i.e. if data is given from 1950 to 2000, subtract 1950 from each year before performing the regression on the data.
Newton's method uses successive approximations to find the root of a function. Though the calculators have much better ways to find roots, Newton's method is still used briefly in calculus classes just for the learning experience. To perform Newton's method on the calculator, put the function to be solved for in y1. Now, go to the home screen, type in your initial guess and hit ENTER. Then use the following equation, which has a few subtle differences depending on which model family calculator you use:
TI-83 family: Ans-Y1(Ans)/nDeriv(Y1,x,Ans)
TI-86: Ans-y1(Ans)/der1(y1,x,Ans)
TI-85: Ans
TI-89 family: x-y1(x)/d(y1(x),x)|x=Ans(1)
Press ENTER repeatedly until the answer stops changing.
Note that it is fairly easy to turn this into a program if you so desire.
There are two ways to perform an implicit derivative (such as the derivative of x^2+y^2) on the TI-89 family calculator. One is to take the derivative in terms of x, replace instances of y with yy, and then put |yy=y(x) on the end. ( | is the "with" symbol, 2nd-K on the 92(+)/V200. The substitution of yy for y is to avoid the circular definition error.) In the result, dy/dx is shown in pretty print as d/dx*(y(x)) and d(y(x),x) on the entry line. You can then manually change the d/dx*(y(x)) into something like dxdy and isolate it using solve().
This substitution method actually allows for some variation. Instead of d(x^2+yy^2,x)|yy=y(x) you can do d(x^2+y(x)^2,x)|d(y(x),x)=y' and y(x)=y which returns quite tidy results in terms of x, y, and y'.
The better way, suggested and explained on one of TI's old FAQ pages, is to create and use this function
-d(uu,xx)/d(uu,yy)impdif(uu,xx,yy)
impdif(x^2+y^2,x,y) gives -x/y
You can also use a program to do what amounts to the same thing. This program by Don Phillips
handles implicit differentiation to the nth degree.
As any good calculus textbook will tell you, the term "partial derivative" only means that when you take the derivative of an equation with more than one variable, you have to do it one variable at a time while treating the other variables as constants. Each partial derivative works exactly the same as a normal derivative of an equation with one variable. Since the derivative command on the 89 family requires that you specify which variable to differentiate by anyway, a partial derivative is performed the same way any derivative is. Just be sure to avoid creating a new variable when you think you're using implied multiplication.
Riemann sums (also known as the Rectangular Approximation Method) are used in calculus to approximate definite integrals that are too complex to use the fundamental theorem of calculus. The following functions for the different model families compute the value of Riemann sums. If you wish to also see the function graphed with the rectangle divisions drawn in, programs for that are available from many places, including the Houghton Mifflin website.
For the TI-89 family:
Though programs have been written to perform these (including the Calculus Tools Flash App
available from TI), all you need is these short functions. Type the following equations at the
home screen, one at a time (note: Sigma is in the F3 CALC menu)
Left hand sum: Sigma(f(a+i*(b-a)/n)*(b-a)/n,i,0,n-1)
a is the left bound, b is the right bound, n is the number of subdivisions, and f(x) is the function. f(x) must be stored beforehand, but the other three variables are passed into the equation as arguments when it is used. For example, to find the midpoint approximation of x^2 from 1 to 5 with 10 subdivisions, type at the home screen:
x^2
For the TI-86:
The same equations work, with some adjustments for the 86's lack of function notation:
Left hand sum: LEFTSUM=sum seq(y1(A+I*(B-A)/N)*(B-A)/N,I,0,N-1) Right hand sum: RIGHTSUM=sum seq(y1(A+I*(B-A)/N)*(B-A)/N,I,1,N) Midpoint sum: MIDSUM=sum seq(y1(A+(B-A)*(2*I+1)/(2*N))*(B-A)/N,I,0,N-1) Trapezoid rule: TRAPSUM=(LEFTSUM+RIGHTSUM)/2 Simpson's rule: SIMPSUM=(2*MIDSUM+TRAPSUM)/3
A is the left bound, B is the right bound, N is the number of subdivisions, and y1 is the function. All four must be stored beforehand. For example, to find the midpoint approximation of x^2 from 1 to 5 with 10 subdivisions, type at the home screen:
y1=x^2 1
It's fairly easy to turn that process into a program if that is more desirable.
For the TI-83 family:
It's the same as the TI-86, except that you can't store equations to anything other than graph
equation variables. It may be advisable to put them all into a program so they're easy to retrieve:
PROGRAM:RIEMANN :Disp "PUT EQN IN Y1" :Disp "Y2=LEFT SUM" :"sum(seq(Y1(A+I*(B-A)/N)*(B-A)/N,I,0,N-1))"
For example, to find the midpoint approximation of x^2 from 1 to 5 with 10 subdivisions, type at the home screen:
"x^2"
It's fairly easy to turn that process into a program if that is more desirable.
For the TI-85:
The same basic equations apply, but due to the lack of function notation the y1(x) would need to
be handled differently, x would need to be an equation itself. There are Riemann sum programs
for the 85 floating around that don't use this method though.
The TI-8x calculators also have an fnInt( command which will compute a definite integral, though according to TI's Knowledge Base it uses the Gauss-Kronrod method instead of Riemann sums (article 13625).
There is no calculator function for finding the volume of a solid of revolution, it's more a matter of knowing how to properly set up the integral. Then you just type that integral into the calculator the same way you do when finding the area under a curve. In general, the equations take the following forms using the function stored in y1 and the limits a and b:
Rotation around the x axis ("Disk/washer method")
pi*fnInt(y1(x)^2,x,a,b)
Rotation around the y axis ("Shell method")
2pi*fnInt(y1(x)*x,x,a,b)
The integral symbol is be used in the place of fnInt( on the TI-89 family.
You may have noticed when tracing graphs that the numbers are all funny decimals. This can be fixed by constructing what has been dubbed a friendly window.
The problem of strange numbers when tracing arises because the default window values for all TI calculators is X: -10 to 10 and Y: -10 to 10. Each axis has a range of 20 digits. The 83 family, for example, has a display 96 by 64 pixels. The pixel at the origin doesn't count and the rightmost column of pixels isn't used, so horizontally each pixel is worth 20/94=.2127659 Since the tracer goes pixel by pixel, the X values traced are in increments of .2127659, leading to hard to read graphs.
To get a friendly window, one must construct the window so that each pixel works out to a nice round value like 1, .5, or .25. Note that the ZoomInteger and ZoomDecimal commands make windows with pixel values of 1 and 0.1, respectively. Creative ZoomIn's or ZoomOut's can adjust the window. On the TI-85/86, which does not have square pixels, follow that up with a ZoomSquare, which throws the Y increments off slightly, but the tracer only follows X values anyway, and then the graphs will look identical to those on paper (i.e. graphed circles appear round on screen). The variables xScl and yScl control the intervals of the tick marks on the axis, change them to suit your tastes. The variable xRes controls the tracer's movements; xRes=1 traces every pixel, xRes=2 traces every other pixel, and so on.
To get to my favorite friendly window of .25 increments, do ZoomInteger, ZoomIn, ZoomSquare, and set xScl, yScl, and xRes to 1. This makes a friendly window that is approximately the same size as the standard window. On most of the calculators you can then store your window settings in the menus so you can quickly recall them later. TI-82 users will have to write a short program to recall their window.
Or, you can do the math yourself. A friendly window of square .25 pixel increments on the 83
family would look like this:
(.25*94)/2=11.75 Xmin=-11.75 Xmax=11.75
(.25*62)/2=7.75 Ymin=-7.75 Ymax=7.75
Using screen size data from TI's website and this method, you can create friendly windows with strange increments, such as 1/3 or some fraction of pi.
Note that the ZoomTrig setting provides a friendly window for trig function graphs, scaled to pi for Radian mode and 180 for Degree mode.
You can depict an inequality by graphing the function as if it were equal to y, and then shading above or below the graphed line. There are graphing styles on the y= screen that will do the shading (except for on the TI-82 and TI-85). All the TI graphing calculators also have the Shade( command. It is entered like this: Shade(lower, upper, [left, right]) Lower and upper are functions defining the lower and upper boundaries of the shaded area. You can type the equation or enter y1 if you have the equation entered as y1 already. You could also enter just a number for the boundary, since a constant is also a function. Left and right are optional left and right boundaries. If you do not specify left and right boundaries, your current window size is used as the default values. However, you still have to decide yourself whether to shade above or below your function, depending on which inequality you are given.
The 83 Flash family also has a flash application for inequality graphing.
For the TI-8x:
To restrict a function to certain x values on a TI-8x calculator, divide the function by the
inequalities that define the boundaries. For example, say you want to graph x^2/4-8 where
2<x<7. Input the function as: y1=(x^2/4-8)/((2<x)(x<7)) When the inequalities conditionals are
true, they result as 1, and division by 1 has no effect. When an inequality is false, it results as 0,
and division by 0 causes an undefined error which does not graph. It is important to enclose the
entire original function in parentheses, otherwise the order of operations may cause unintended
results.
To create a piecemeal function on one y= line with TI-8x calculators, multiply each piece of the function by the inequality and add them all together. For example: y1=(x^2)(x<0)+(x)(x>=0) where >= is the greater than or equal to sign. Once again, do not forget the parentheses. The pieces that are not true for a given x value contribute 0 to the sum. Make sure no inequalities overlap, or the graph will not come out right.
The inequalities can be used with anything from the test menu, and can even use boolean operators. For example, (x<2 or x>5). To put x in between two values such as 0<x<2 you must split it into two inequalities like so: (0<x and x<2).
For the TI-89 family:
To restrict x values on a TI-89 family calculator, instead of dividing by the inequality use the
"with" symbol ( |, 2nd-K on the 92(+)/V200) in between the equation and the inequality. Boolean
operators must be used to combine inequality conditions instead of multiplication. For example,
say you want to graph x^2/4-8 where 2<x<7. Input the function as: y1=x^2/4-8|2<x and x<7 The
inequality conditionals result in "true" or "false", with "false" preventing graphing at that x value.
The 89 family will do piecemeal graphs on a single line by using the when() command. It is used as follows: when(inequality for equation 1, equation 1, equation 2). For example: y1=when(x<0, x^2,x) For three equations, another when( command can be nested in the place of equation 2.
Since x= does not define a function (it does not always pass the vertical line test), it will not
graph the same way. Say you want to graph x=y^2. You can solve it for y as
y={1,-1}x. You can DrawInverse x^2, since the inverse of the inverse
makes the original. The DrawInverse command is in the Graph Draw menu. You can also use
parametric graphing mode. Set yt1=t and xt1=t^2. (Since y=t, it's like saying xt1=y^2.) Just
remember to adjust the values of tMin and tMax to allow for the range of y values you want.
If a vertical line is all that is desired, there is also a vertical line command under the Graph Draw menu. Or you can graph y=10^50*(x-N) where N is the x value where you want the line. The slope in this equation is so large that the function will be so darn near vertical that you won't notice it isn't.
Rearrange the standard conic formula Ax2+Bxy+Cy2+Dx+Ey+F=0
to get Cy2+(Bx+E)y+(Ax2+Dx+F)=0
You can see how the conic formula now resembles a quadratic equation with y as the variable in question instead of x. Now follow along depending on which model family calculator you have:
For the TI-83 family:
Input the following into the Y= screen, substituting the numbers from your conic equation for the
letters shown in red:
Y1=C
Y2=BX+E
Y3=AX2+DX+F
Y4=(-Y2+{1,-1}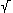(Y22-4Y1Y3))/(2Y1)
(The Y characters are found in the VARS menu.) Now deselect Y1 through 3 so they don't show up, and graph it.
For the TI-85/86:
Store the following from the home screen, substituting the numbers from your conic equation for
the letters shown in red:
A=C
B=Bx+E
C=Ax2+Dx+F
QUAD=(-B+{1,-1}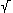(B2-4*A*C))/(2A)
Now set y1=QUAD, and graph it.
For the TI-89 family:
Store the following from the home screen, substituting the numbers from your conic equation for
the letters shown in red:
C
Now set y1(x)=quad(x), and graph it.
Example: If your conic is 2x2+3xy+4y2+5x+6y+7=0
you would store A=4, B=3x+6, C=2x^2+5x+7
(Note: This is not a real conic, just an example using numbers I made up.)
What this does is solve for y in the conic formula by using the quadratic equation. For a little less typing, you can always put the first three equations right into the quadratic equation, but keeping them separate makes it easier to change the numbers later on if you have several conics to do. Note that it is fairly easy to turn this into a program if you so desire.
Alternate method for the TI-89 Flash family:
Implicit graphing is a built-in feature. In 3D graph mode, go to the Graph Format menu and set Style to Implicit Plot. Adjust the window so you are looking down upon the x-y plane along the z axis. Enter the equation in terms of x and y as z1 and graph it.
There are two ways to do this, one in function mode and the other in parametric mode. In function mode, to get the x axis on a logarithmic scale, set y=f(10^x) where f(x) is your function. You can do this by substituting (10^x) for every instance of x in the equation. For the y axis on a logarithmic scale, set y=log(f(x)). For both, use y=log(f(10^x)).
A similar method uses parametric mode. Set xt1=log(t) and yt1=log(f(t)) in which f(t) is your function in terms of t. If you want the logarithmic scale on only one axis, do the same thing but only use log on one of them. Of course, ln can be used instead of log depending on the scale you want. Do not forget to adjust tMin, tMax, and tStep to suit your needs.
One traditional way of depicting complex numbers is to designate the x-axis as the real portion of the number and the y-axis as the imaginary portion. A function involving complex elements can be graphed in this manner using parametric graphing. Set xt1=real(f(t)) and yt1=imag(f(t)) where f(t) is the function.
Graphing the second derivative of a function is fairly straightforward on the 89 family and the
85/86, you just use d() with a third argument of 2 or der2(), respectively. For the 83 family, it
requires a bit of a kludge. Where f(x) is the function, enter
Y1=nDeriv(f(x),X,X)
Y2=nDeriv(Y1,X,X)
and only select Y2 for graphing. Do not type out Y1, take it from the VARS menu.
On line since Sept. 1997 |
|
|
NOTICE: This site has no legal affiliation with Texas Instruments Incorporated. The owners and
operators of this site are solely responsible and liable for any content or goods on or obtained
from this site. Texas Instruments Incorporated ("TI") makes no representation with respect to the
suitability of any of the information contained in any content or non-TI goods obtained from this
site. In no event shall TI or its licensees be liable for any damages whatsoever, including special,
indirect or consequential damages, arising out of or in connection with the use of or performance
of the content or non-TI goods obtained from this site.
Voyage 200 is a trademark of Texas Instruments.
